library(tidyverse)
library(easystats)
library(rstan)
library(rstanarm)
cat_weights <- tibble(avg_daily_snacks = c(3, 2, 4, 2, 3, 1, 1, 0, 1, 0, 2, 3, 1, 2, 1, 3),
weight = c(3.8, 3.9, 5, 3.7, 4.1, 3.6, 3.7, 3.6, 3.8, 4.1, 4.3, 3.9, 3.7, 3.8, 3.5, 4.3),
environ = c("Indoor", "Indoor", "Outdoor", "Indoor",
"Outdoor", "Indoor", "Outdoor", "Indoor",
"Indoor", "Indoor", "Outdoor", "Indoor",
"Outdoor", "Indoor", "Indoor", "Outdoor"))4 Week 3: Introduction to Analyses
Lecture 2: Introduction to statistics
Set up your environment and packages
Summarise example data
cat_weights |>
summarise("Mean Weight (kg)" = mean(weight),
"SD Weight (kg)" = sd(weight),
"Mean Daily Snacks" = mean (avg_daily_snacks),
)# A tibble: 1 × 3
`Mean Weight (kg)` `SD Weight (kg)` `Mean Daily Snacks`
<dbl> <dbl> <dbl>
1 3.92 0.373 1.81Visualise example data
cat_weights |>
ggplot(aes(x = avg_daily_snacks, y = weight)) +
geom_point() +
labs(x = "Average Daily Snacks", y = "Cat Weight") +
theme_classic() +
scale_y_continuous(limits = c(0,5))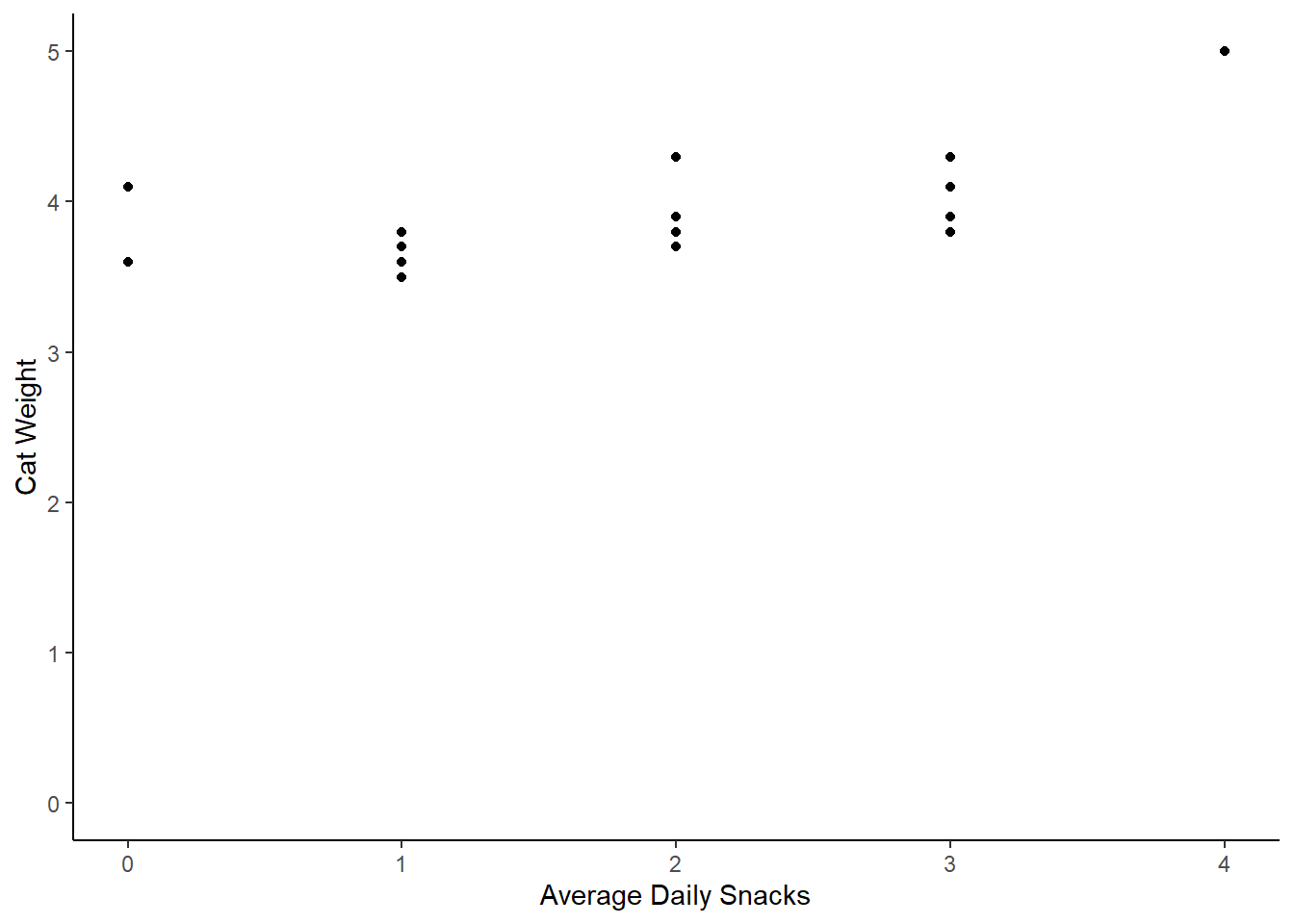
A Linear Model
model_fcat <- lm(weight ~ avg_daily_snacks, data = cat_weights)
summary(model_fcat)
Call:
lm(formula = weight ~ avg_daily_snacks, data = cat_weights)
Residuals:
Min 1Q Median 3Q Max
-0.36758 -0.18723 -0.06116 0.06705 0.62813
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.55474 0.14045 25.309 4.33e-13 ***
avg_daily_snacks 0.20428 0.06576 3.107 0.00773 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.2973 on 14 degrees of freedom
Multiple R-squared: 0.4081, Adjusted R-squared: 0.3658
F-statistic: 9.652 on 1 and 14 DF, p-value: 0.007729report::report(model_fcat)We fitted a linear model (estimated using OLS) to predict weight with
avg_daily_snacks (formula: weight ~ avg_daily_snacks). The model explains a
statistically significant and substantial proportion of variance (R2 = 0.41,
F(1, 14) = 9.65, p = 0.008, adj. R2 = 0.37). The model's intercept,
corresponding to avg_daily_snacks = 0, is at 3.55 (95% CI [3.25, 3.86], t(14) =
25.31, p < .001). Within this model:
- The effect of avg daily snacks is statistically significant and positive
(beta = 0.20, 95% CI [0.06, 0.35], t(14) = 3.11, p = 0.008; Std. beta = 0.64,
95% CI [0.20, 1.08])
Standardized parameters were obtained by fitting the model on a standardized
version of the dataset. 95% Confidence Intervals (CIs) and p-values were
computed using a Wald t-distribution approximation.parameters(model_fcat) Parameter | Coefficient | SE | 95% CI | t(14) | p
---------------------------------------------------------------------
(Intercept) | 3.55 | 0.14 | [3.25, 3.86] | 25.31 | < .001
avg daily snacks | 0.20 | 0.07 | [0.06, 0.35] | 3.11 | 0.008 plot(model_parameters(model_fcat), show_intercept = TRUE)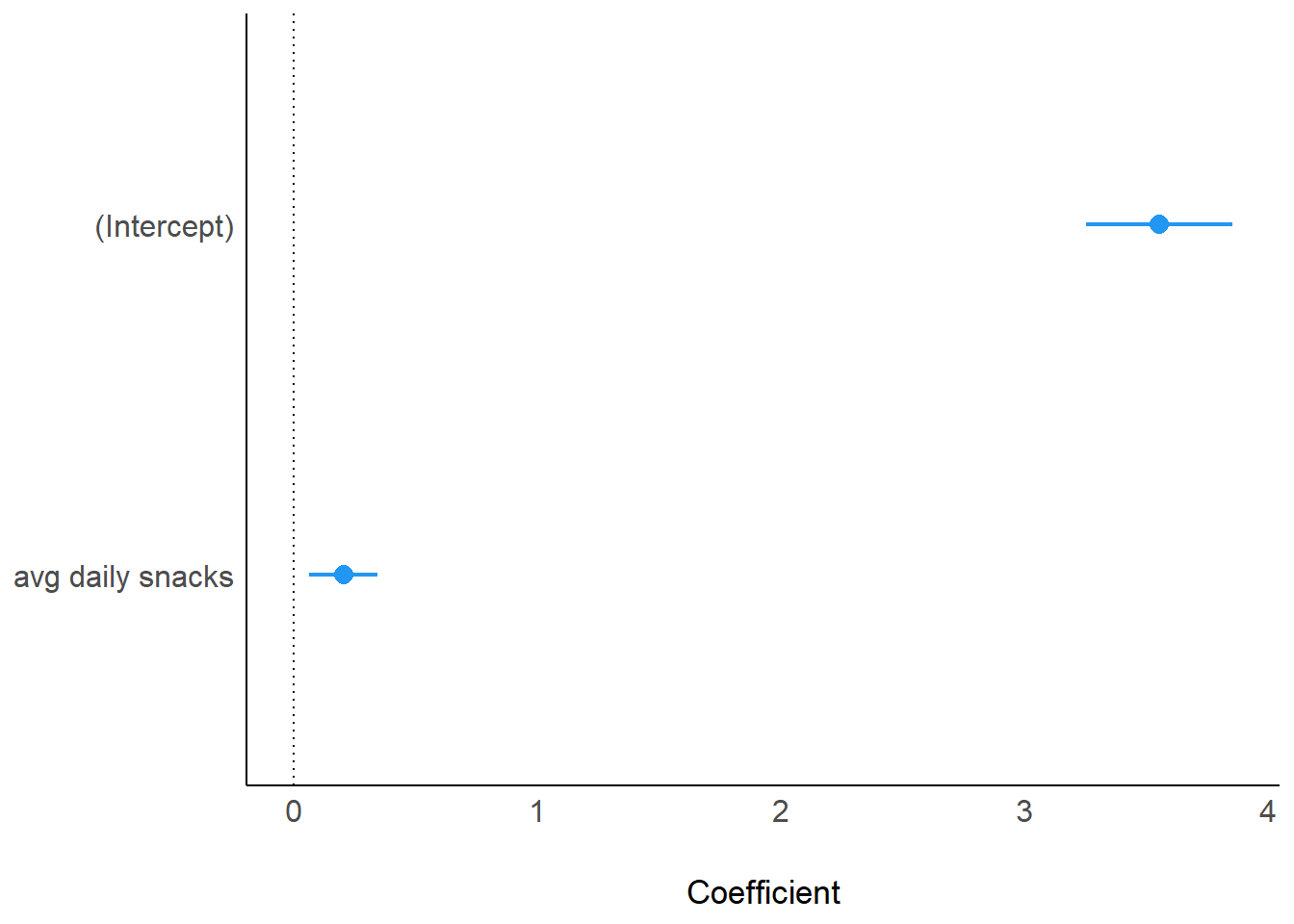
plot(model_parameters(model_fcat))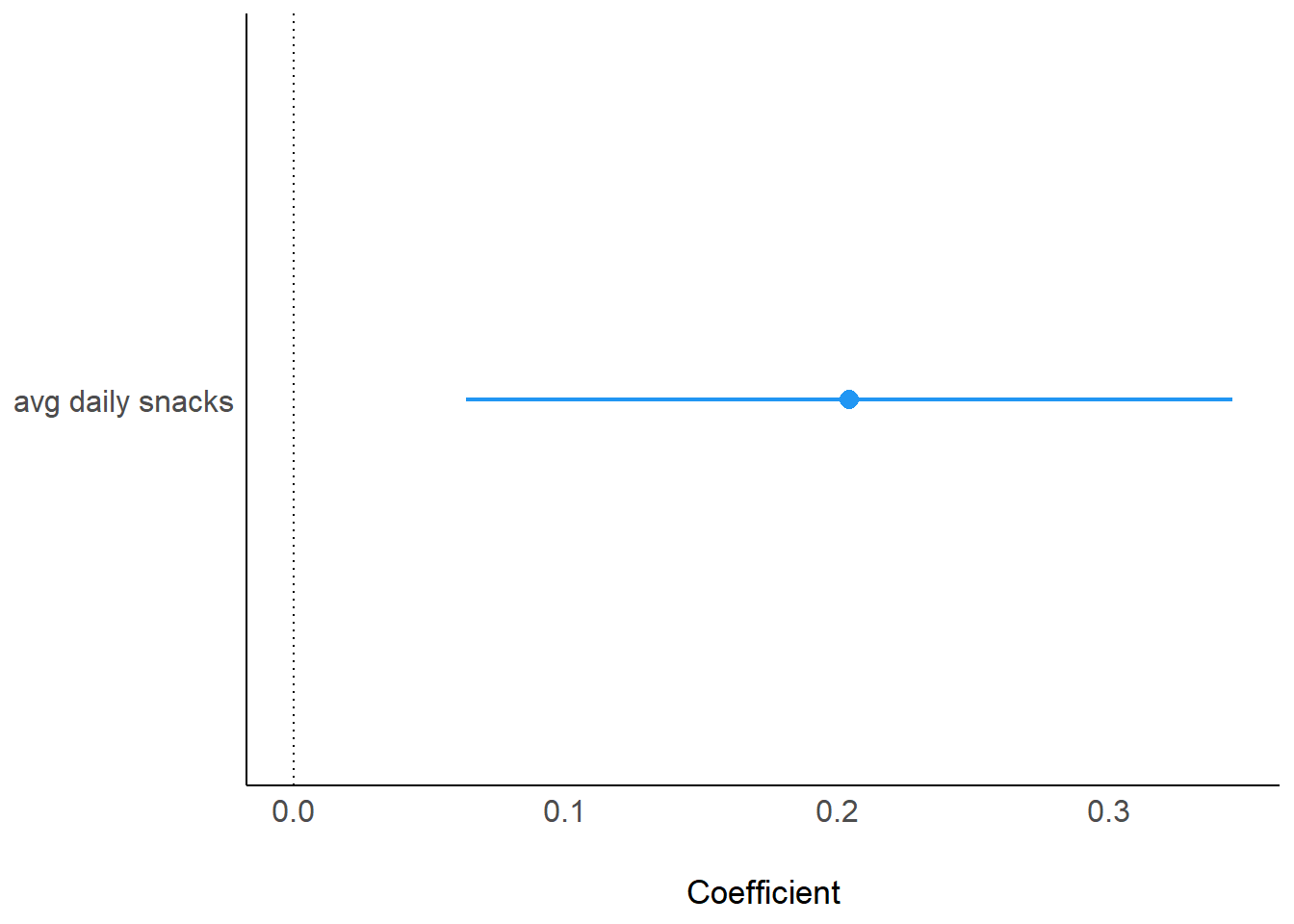
cat_weights |>
ggplot(aes(x = avg_daily_snacks, y = weight)) +
geom_point() +
labs(x = "Average Daily Snacks", y = "Cat Weight",
caption = "Weight ~ Average Daily Snacks shown") +
theme_classic() +
scale_y_continuous(limits = c(0,5)) +
geom_abline(slope = 0.20, intercept = 3.55)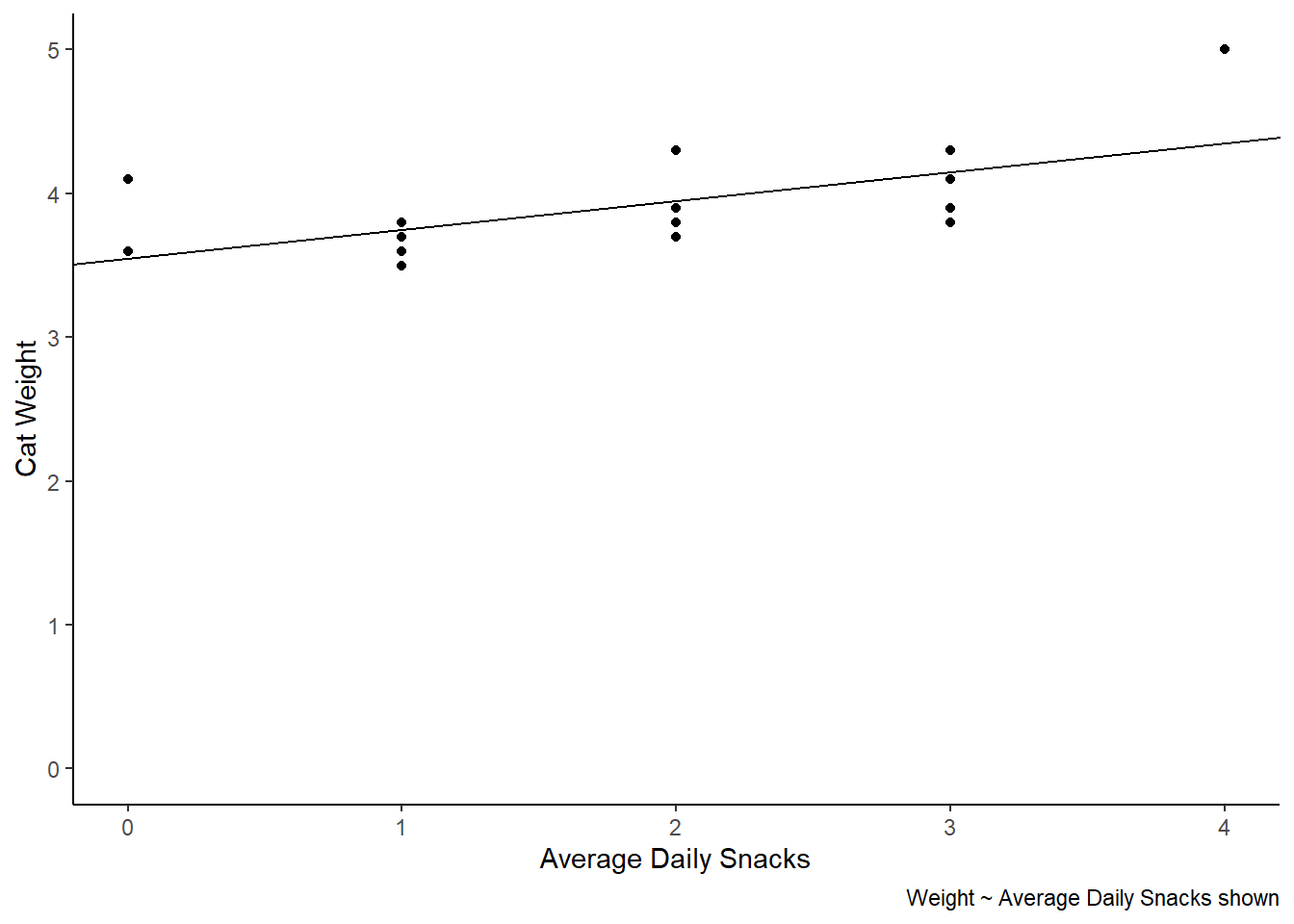
A Bayesian Model
set.seed(10)
model_bcat <- stan_glm(weight ~ avg_daily_snacks, data = cat_weights)
SAMPLING FOR MODEL 'continuous' NOW (CHAIN 1).
Chain 1:
Chain 1: Gradient evaluation took 5.6e-05 seconds
Chain 1: 1000 transitions using 10 leapfrog steps per transition would take 0.56 seconds.
Chain 1: Adjust your expectations accordingly!
Chain 1:
Chain 1:
Chain 1: Iteration: 1 / 2000 [ 0%] (Warmup)
Chain 1: Iteration: 200 / 2000 [ 10%] (Warmup)
Chain 1: Iteration: 400 / 2000 [ 20%] (Warmup)
Chain 1: Iteration: 600 / 2000 [ 30%] (Warmup)
Chain 1: Iteration: 800 / 2000 [ 40%] (Warmup)
Chain 1: Iteration: 1000 / 2000 [ 50%] (Warmup)
Chain 1: Iteration: 1001 / 2000 [ 50%] (Sampling)
Chain 1: Iteration: 1200 / 2000 [ 60%] (Sampling)
Chain 1: Iteration: 1400 / 2000 [ 70%] (Sampling)
Chain 1: Iteration: 1600 / 2000 [ 80%] (Sampling)
Chain 1: Iteration: 1800 / 2000 [ 90%] (Sampling)
Chain 1: Iteration: 2000 / 2000 [100%] (Sampling)
Chain 1:
Chain 1: Elapsed Time: 0.05 seconds (Warm-up)
Chain 1: 0.053 seconds (Sampling)
Chain 1: 0.103 seconds (Total)
Chain 1:
SAMPLING FOR MODEL 'continuous' NOW (CHAIN 2).
Chain 2:
Chain 2: Gradient evaluation took 1.4e-05 seconds
Chain 2: 1000 transitions using 10 leapfrog steps per transition would take 0.14 seconds.
Chain 2: Adjust your expectations accordingly!
Chain 2:
Chain 2:
Chain 2: Iteration: 1 / 2000 [ 0%] (Warmup)
Chain 2: Iteration: 200 / 2000 [ 10%] (Warmup)
Chain 2: Iteration: 400 / 2000 [ 20%] (Warmup)
Chain 2: Iteration: 600 / 2000 [ 30%] (Warmup)
Chain 2: Iteration: 800 / 2000 [ 40%] (Warmup)
Chain 2: Iteration: 1000 / 2000 [ 50%] (Warmup)
Chain 2: Iteration: 1001 / 2000 [ 50%] (Sampling)
Chain 2: Iteration: 1200 / 2000 [ 60%] (Sampling)
Chain 2: Iteration: 1400 / 2000 [ 70%] (Sampling)
Chain 2: Iteration: 1600 / 2000 [ 80%] (Sampling)
Chain 2: Iteration: 1800 / 2000 [ 90%] (Sampling)
Chain 2: Iteration: 2000 / 2000 [100%] (Sampling)
Chain 2:
Chain 2: Elapsed Time: 0.037 seconds (Warm-up)
Chain 2: 0.042 seconds (Sampling)
Chain 2: 0.079 seconds (Total)
Chain 2:
SAMPLING FOR MODEL 'continuous' NOW (CHAIN 3).
Chain 3:
Chain 3: Gradient evaluation took 1.3e-05 seconds
Chain 3: 1000 transitions using 10 leapfrog steps per transition would take 0.13 seconds.
Chain 3: Adjust your expectations accordingly!
Chain 3:
Chain 3:
Chain 3: Iteration: 1 / 2000 [ 0%] (Warmup)
Chain 3: Iteration: 200 / 2000 [ 10%] (Warmup)
Chain 3: Iteration: 400 / 2000 [ 20%] (Warmup)
Chain 3: Iteration: 600 / 2000 [ 30%] (Warmup)
Chain 3: Iteration: 800 / 2000 [ 40%] (Warmup)
Chain 3: Iteration: 1000 / 2000 [ 50%] (Warmup)
Chain 3: Iteration: 1001 / 2000 [ 50%] (Sampling)
Chain 3: Iteration: 1200 / 2000 [ 60%] (Sampling)
Chain 3: Iteration: 1400 / 2000 [ 70%] (Sampling)
Chain 3: Iteration: 1600 / 2000 [ 80%] (Sampling)
Chain 3: Iteration: 1800 / 2000 [ 90%] (Sampling)
Chain 3: Iteration: 2000 / 2000 [100%] (Sampling)
Chain 3:
Chain 3: Elapsed Time: 0.046 seconds (Warm-up)
Chain 3: 0.055 seconds (Sampling)
Chain 3: 0.101 seconds (Total)
Chain 3:
SAMPLING FOR MODEL 'continuous' NOW (CHAIN 4).
Chain 4:
Chain 4: Gradient evaluation took 0.000578 seconds
Chain 4: 1000 transitions using 10 leapfrog steps per transition would take 5.78 seconds.
Chain 4: Adjust your expectations accordingly!
Chain 4:
Chain 4:
Chain 4: Iteration: 1 / 2000 [ 0%] (Warmup)
Chain 4: Iteration: 200 / 2000 [ 10%] (Warmup)
Chain 4: Iteration: 400 / 2000 [ 20%] (Warmup)
Chain 4: Iteration: 600 / 2000 [ 30%] (Warmup)
Chain 4: Iteration: 800 / 2000 [ 40%] (Warmup)
Chain 4: Iteration: 1000 / 2000 [ 50%] (Warmup)
Chain 4: Iteration: 1001 / 2000 [ 50%] (Sampling)
Chain 4: Iteration: 1200 / 2000 [ 60%] (Sampling)
Chain 4: Iteration: 1400 / 2000 [ 70%] (Sampling)
Chain 4: Iteration: 1600 / 2000 [ 80%] (Sampling)
Chain 4: Iteration: 1800 / 2000 [ 90%] (Sampling)
Chain 4: Iteration: 2000 / 2000 [100%] (Sampling)
Chain 4:
Chain 4: Elapsed Time: 0.054 seconds (Warm-up)
Chain 4: 0.063 seconds (Sampling)
Chain 4: 0.117 seconds (Total)
Chain 4: summary(model_bcat)
Model Info:
function: stan_glm
family: gaussian [identity]
formula: weight ~ avg_daily_snacks
algorithm: sampling
sample: 4000 (posterior sample size)
priors: see help('prior_summary')
observations: 16
predictors: 2
Estimates:
mean sd 10% 50% 90%
(Intercept) 3.6 0.2 3.4 3.6 3.7
avg_daily_snacks 0.2 0.1 0.1 0.2 0.3
sigma 0.3 0.1 0.2 0.3 0.4
Fit Diagnostics:
mean sd 10% 50% 90%
mean_PPD 3.9 0.1 3.8 3.9 4.1
The mean_ppd is the sample average posterior predictive distribution of the outcome variable (for details see help('summary.stanreg')).
MCMC diagnostics
mcse Rhat n_eff
(Intercept) 0.0 1.0 3066
avg_daily_snacks 0.0 1.0 2981
sigma 0.0 1.0 2539
mean_PPD 0.0 1.0 3573
log-posterior 0.0 1.0 1450
For each parameter, mcse is Monte Carlo standard error, n_eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence Rhat=1).describe_posterior(model_bcat)Summary of Posterior Distribution
Parameter | Median | 95% CI | pd | ROPE | % in ROPE | Rhat | ESS
-----------------------------------------------------------------------------------------------
(Intercept) | 3.55 | [3.26, 3.86] | 100% | [-0.04, 0.04] | 0% | 1.001 | 3066.00
avg_daily_snacks | 0.20 | [0.06, 0.35] | 99.62% | [-0.04, 0.04] | 0% | 1.000 | 2981.00report::report(model_bcat)
SAMPLING FOR MODEL 'continuous' NOW (CHAIN 1).
Chain 1:
Chain 1: Gradient evaluation took 1.5e-05 seconds
Chain 1: 1000 transitions using 10 leapfrog steps per transition would take 0.15 seconds.
Chain 1: Adjust your expectations accordingly!
Chain 1:
Chain 1:
Chain 1: Iteration: 1 / 2000 [ 0%] (Warmup)
Chain 1: Iteration: 200 / 2000 [ 10%] (Warmup)
Chain 1: Iteration: 400 / 2000 [ 20%] (Warmup)
Chain 1: Iteration: 600 / 2000 [ 30%] (Warmup)
Chain 1: Iteration: 800 / 2000 [ 40%] (Warmup)
Chain 1: Iteration: 1000 / 2000 [ 50%] (Warmup)
Chain 1: Iteration: 1001 / 2000 [ 50%] (Sampling)
Chain 1: Iteration: 1200 / 2000 [ 60%] (Sampling)
Chain 1: Iteration: 1400 / 2000 [ 70%] (Sampling)
Chain 1: Iteration: 1600 / 2000 [ 80%] (Sampling)
Chain 1: Iteration: 1800 / 2000 [ 90%] (Sampling)
Chain 1: Iteration: 2000 / 2000 [100%] (Sampling)
Chain 1:
Chain 1: Elapsed Time: 0.049 seconds (Warm-up)
Chain 1: 0.058 seconds (Sampling)
Chain 1: 0.107 seconds (Total)
Chain 1:
SAMPLING FOR MODEL 'continuous' NOW (CHAIN 2).
Chain 2:
Chain 2: Gradient evaluation took 1e-05 seconds
Chain 2: 1000 transitions using 10 leapfrog steps per transition would take 0.1 seconds.
Chain 2: Adjust your expectations accordingly!
Chain 2:
Chain 2:
Chain 2: Iteration: 1 / 2000 [ 0%] (Warmup)
Chain 2: Iteration: 200 / 2000 [ 10%] (Warmup)
Chain 2: Iteration: 400 / 2000 [ 20%] (Warmup)
Chain 2: Iteration: 600 / 2000 [ 30%] (Warmup)
Chain 2: Iteration: 800 / 2000 [ 40%] (Warmup)
Chain 2: Iteration: 1000 / 2000 [ 50%] (Warmup)
Chain 2: Iteration: 1001 / 2000 [ 50%] (Sampling)
Chain 2: Iteration: 1200 / 2000 [ 60%] (Sampling)
Chain 2: Iteration: 1400 / 2000 [ 70%] (Sampling)
Chain 2: Iteration: 1600 / 2000 [ 80%] (Sampling)
Chain 2: Iteration: 1800 / 2000 [ 90%] (Sampling)
Chain 2: Iteration: 2000 / 2000 [100%] (Sampling)
Chain 2:
Chain 2: Elapsed Time: 0.037 seconds (Warm-up)
Chain 2: 0.047 seconds (Sampling)
Chain 2: 0.084 seconds (Total)
Chain 2:
SAMPLING FOR MODEL 'continuous' NOW (CHAIN 3).
Chain 3:
Chain 3: Gradient evaluation took 1e-05 seconds
Chain 3: 1000 transitions using 10 leapfrog steps per transition would take 0.1 seconds.
Chain 3: Adjust your expectations accordingly!
Chain 3:
Chain 3:
Chain 3: Iteration: 1 / 2000 [ 0%] (Warmup)
Chain 3: Iteration: 200 / 2000 [ 10%] (Warmup)
Chain 3: Iteration: 400 / 2000 [ 20%] (Warmup)
Chain 3: Iteration: 600 / 2000 [ 30%] (Warmup)
Chain 3: Iteration: 800 / 2000 [ 40%] (Warmup)
Chain 3: Iteration: 1000 / 2000 [ 50%] (Warmup)
Chain 3: Iteration: 1001 / 2000 [ 50%] (Sampling)
Chain 3: Iteration: 1200 / 2000 [ 60%] (Sampling)
Chain 3: Iteration: 1400 / 2000 [ 70%] (Sampling)
Chain 3: Iteration: 1600 / 2000 [ 80%] (Sampling)
Chain 3: Iteration: 1800 / 2000 [ 90%] (Sampling)
Chain 3: Iteration: 2000 / 2000 [100%] (Sampling)
Chain 3:
Chain 3: Elapsed Time: 0.037 seconds (Warm-up)
Chain 3: 0.047 seconds (Sampling)
Chain 3: 0.084 seconds (Total)
Chain 3:
SAMPLING FOR MODEL 'continuous' NOW (CHAIN 4).
Chain 4:
Chain 4: Gradient evaluation took 1e-05 seconds
Chain 4: 1000 transitions using 10 leapfrog steps per transition would take 0.1 seconds.
Chain 4: Adjust your expectations accordingly!
Chain 4:
Chain 4:
Chain 4: Iteration: 1 / 2000 [ 0%] (Warmup)
Chain 4: Iteration: 200 / 2000 [ 10%] (Warmup)
Chain 4: Iteration: 400 / 2000 [ 20%] (Warmup)
Chain 4: Iteration: 600 / 2000 [ 30%] (Warmup)
Chain 4: Iteration: 800 / 2000 [ 40%] (Warmup)
Chain 4: Iteration: 1000 / 2000 [ 50%] (Warmup)
Chain 4: Iteration: 1001 / 2000 [ 50%] (Sampling)
Chain 4: Iteration: 1200 / 2000 [ 60%] (Sampling)
Chain 4: Iteration: 1400 / 2000 [ 70%] (Sampling)
Chain 4: Iteration: 1600 / 2000 [ 80%] (Sampling)
Chain 4: Iteration: 1800 / 2000 [ 90%] (Sampling)
Chain 4: Iteration: 2000 / 2000 [100%] (Sampling)
Chain 4:
Chain 4: Elapsed Time: 0.038 seconds (Warm-up)
Chain 4: 0.055 seconds (Sampling)
Chain 4: 0.093 seconds (Total)
Chain 4: We fitted a Bayesian linear model (estimated using MCMC sampling with 4 chains
of 2000 iterations and a warmup of 1000) to predict weight with
avg_daily_snacks (formula: weight ~ avg_daily_snacks). Priors over parameters
were set as normal (mean = 0.00, SD = 0.80) distributions. The model's
explanatory power is substantial (R2 = 0.38, 95% CI [6.54e-06, 0.62], adj. R2 =
0.15). The model's intercept, corresponding to avg_daily_snacks = 0, is at 3.55
(95% CI [3.26, 3.86]). Within this model:
- The effect of avg daily snacks (Median = 0.20, 95% CI [0.06, 0.35]) has a
99.62% probability of being positive (> 0), 99.30% of being significant (>
0.02), and 90.10% of being large (> 0.11). The estimation successfully
converged (Rhat = 1.000) and the indices are reliable (ESS = 2981)
Following the Sequential Effect eXistence and sIgnificance Testing (SEXIT)
framework, we report the median of the posterior distribution and its 95% CI
(Highest Density Interval), along the probability of direction (pd), the
probability of significance and the probability of being large. The thresholds
beyond which the effect is considered as significant (i.e., non-negligible) and
large are |0.02| and |0.11| (corresponding respectively to 0.05 and 0.30 of the
outcome's SD). Convergence and stability of the Bayesian sampling has been
assessed using R-hat, which should be below 1.01 (Vehtari et al., 2019), and
Effective Sample Size (ESS), which should be greater than 1000 (Burkner, 2017).posteriors <- get_parameters(model_bcat)
posteriors |>
ggplot(aes(x = avg_daily_snacks)) +
geom_density(fill = "lightblue") +
theme_classic() +
labs(x = "Posterior Coefficient Estimates for Average Daily Snacks",
y = "Density",
caption = "Median Estimate Shown") +
geom_vline(xintercept = 0.21, color = "darkblue", linewidth = 1)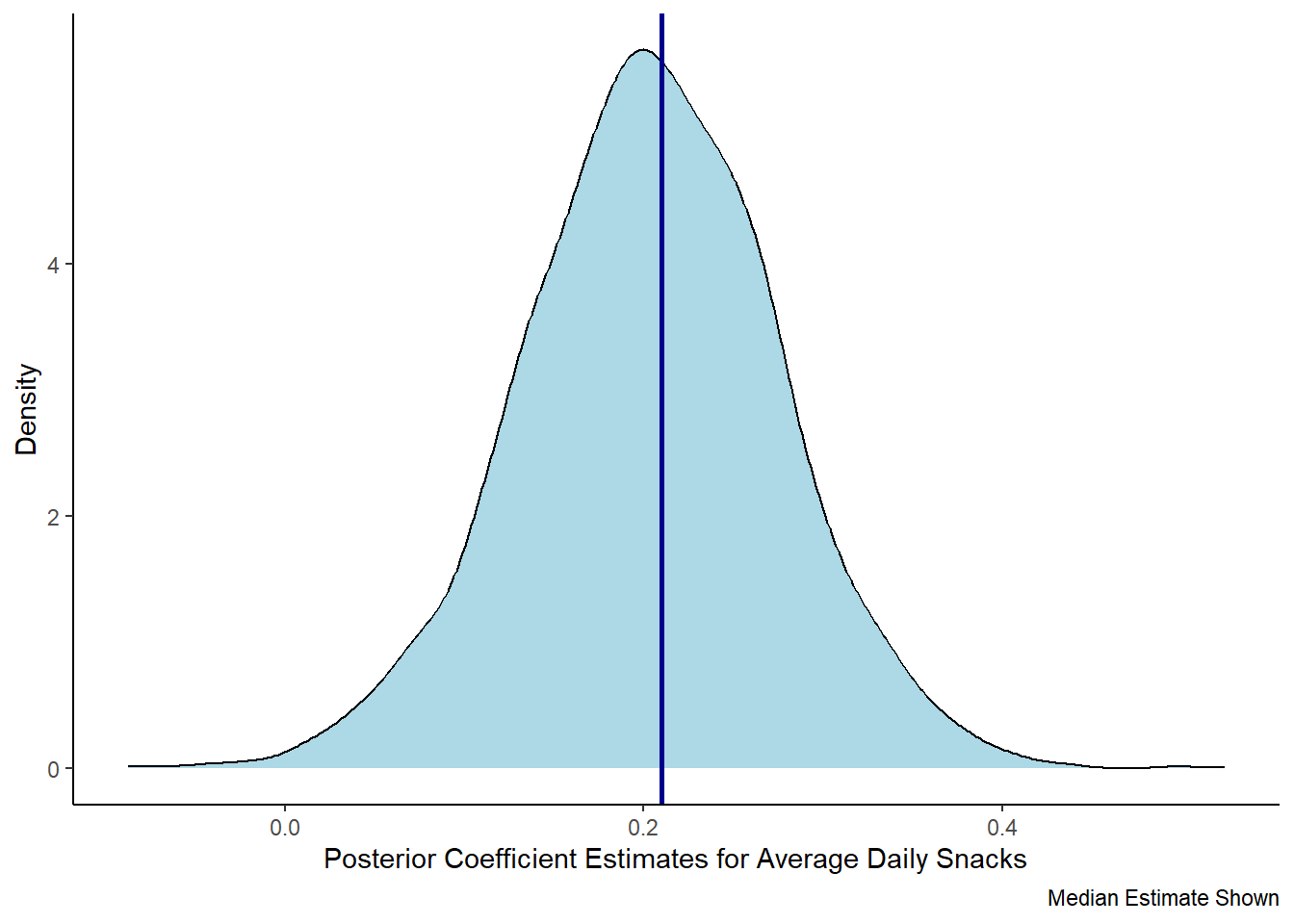
A Linear model with a factor
model_fcat2 <- lm(weight ~ avg_daily_snacks + environ, data = cat_weights)
summary(model_fcat2)
Call:
lm(formula = weight ~ avg_daily_snacks + environ, data = cat_weights)
Residuals:
Min 1Q Median 3Q Max
-0.2678 -0.1897 -0.0700 0.0821 0.5725
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.52748 0.13078 26.972 8.49e-13 ***
avg_daily_snacks 0.16168 0.06512 2.483 0.0275 *
environOutdoor 0.27860 0.15203 1.833 0.0899 .
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.275 on 13 degrees of freedom
Multiple R-squared: 0.5296, Adjusted R-squared: 0.4572
F-statistic: 7.318 on 2 and 13 DF, p-value: 0.007431report::report(model_fcat2)We fitted a linear model (estimated using OLS) to predict weight with
avg_daily_snacks and environ (formula: weight ~ avg_daily_snacks + environ).
The model explains a statistically significant and substantial proportion of
variance (R2 = 0.53, F(2, 13) = 7.32, p = 0.007, adj. R2 = 0.46). The model's
intercept, corresponding to avg_daily_snacks = 0 and environ = Indoor, is at
3.53 (95% CI [3.24, 3.81], t(13) = 26.97, p < .001). Within this model:
- The effect of avg daily snacks is statistically significant and positive
(beta = 0.16, 95% CI [0.02, 0.30], t(13) = 2.48, p = 0.027; Std. beta = 0.51,
95% CI [0.07, 0.95])
- The effect of environ [Outdoor] is statistically non-significant and positive
(beta = 0.28, 95% CI [-0.05, 0.61], t(13) = 1.83, p = 0.090; Std. beta = 0.75,
95% CI [-0.13, 1.63])
Standardized parameters were obtained by fitting the model on a standardized
version of the dataset. 95% Confidence Intervals (CIs) and p-values were
computed using a Wald t-distribution approximation.parameters(model_fcat2)Parameter | Coefficient | SE | 95% CI | t(13) | p
-----------------------------------------------------------------------
(Intercept) | 3.53 | 0.13 | [ 3.24, 3.81] | 26.97 | < .001
avg daily snacks | 0.16 | 0.07 | [ 0.02, 0.30] | 2.48 | 0.027
environ [Outdoor] | 0.28 | 0.15 | [-0.05, 0.61] | 1.83 | 0.090 plot(model_parameters(model_fcat2), show_intercept = TRUE)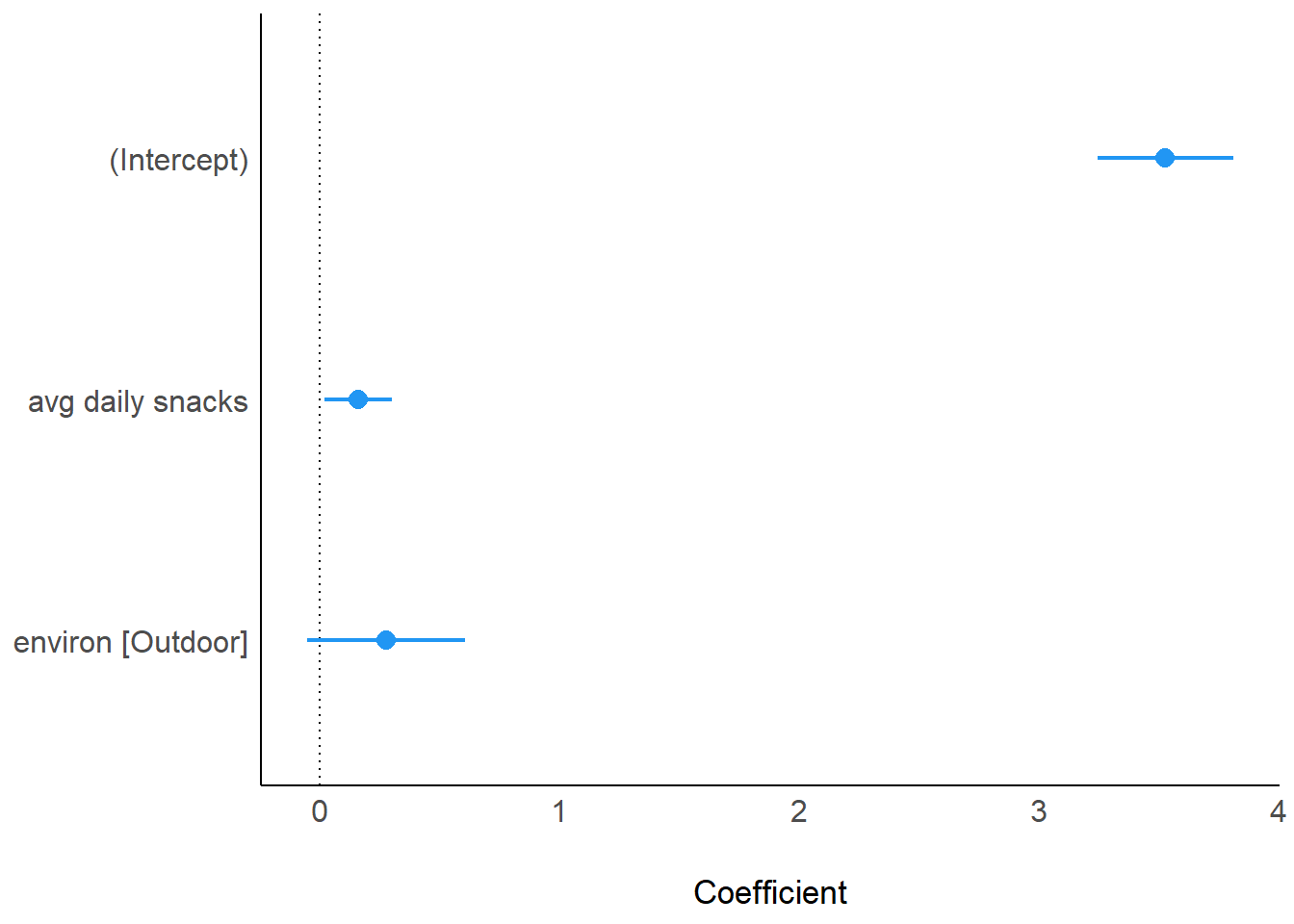
plot(model_parameters(model_fcat2))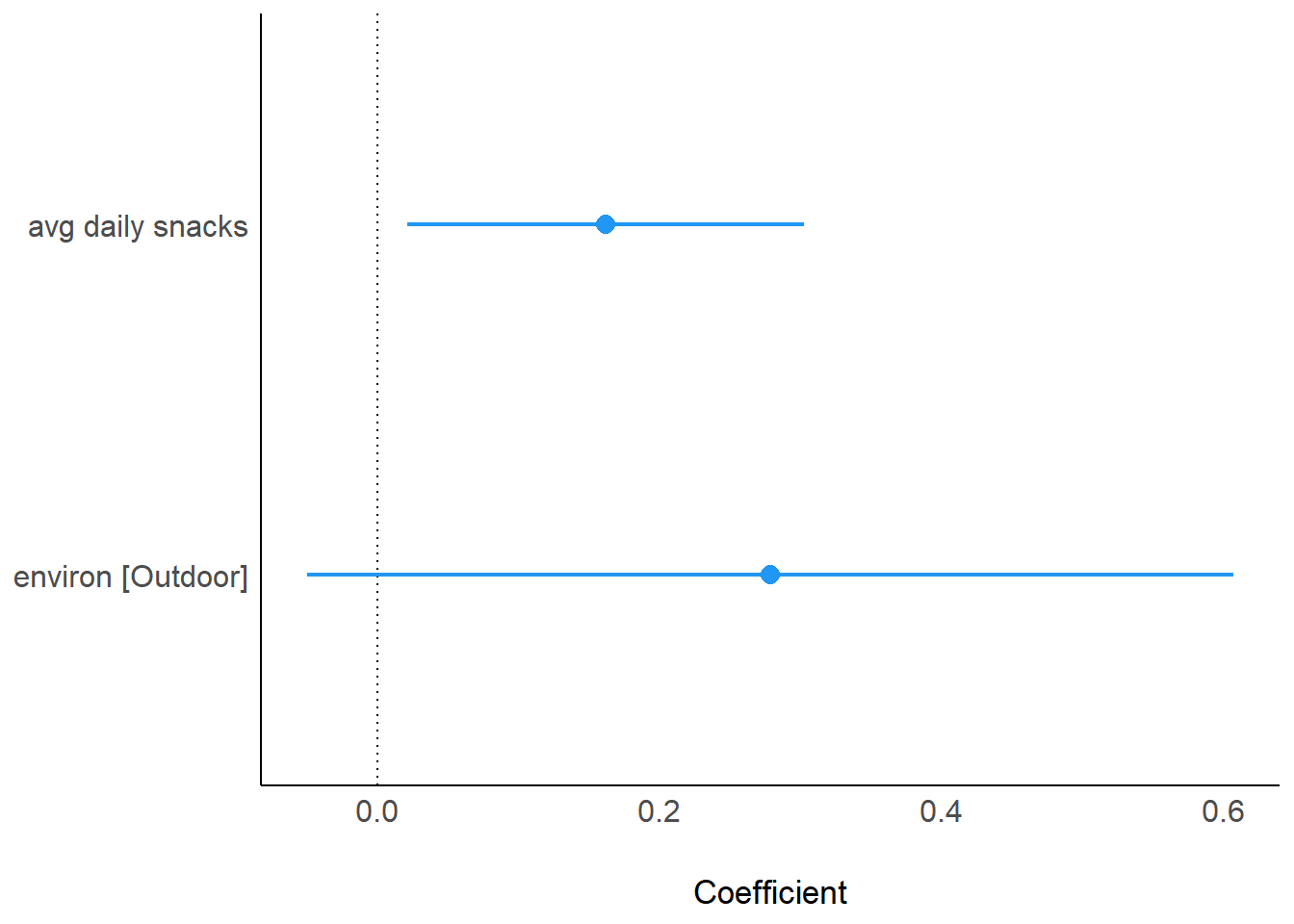
cat_weights |>
ggplot(aes(x = avg_daily_snacks, y = weight, colour = environ)) +
geom_point() +
labs(x = "Average Daily Snacks", y = "Cat Weight",
caption = "Weight ~ Average Daily Snacks shown") +
theme_classic() +
scale_y_continuous(limits = c(0,5)) +
geom_smooth()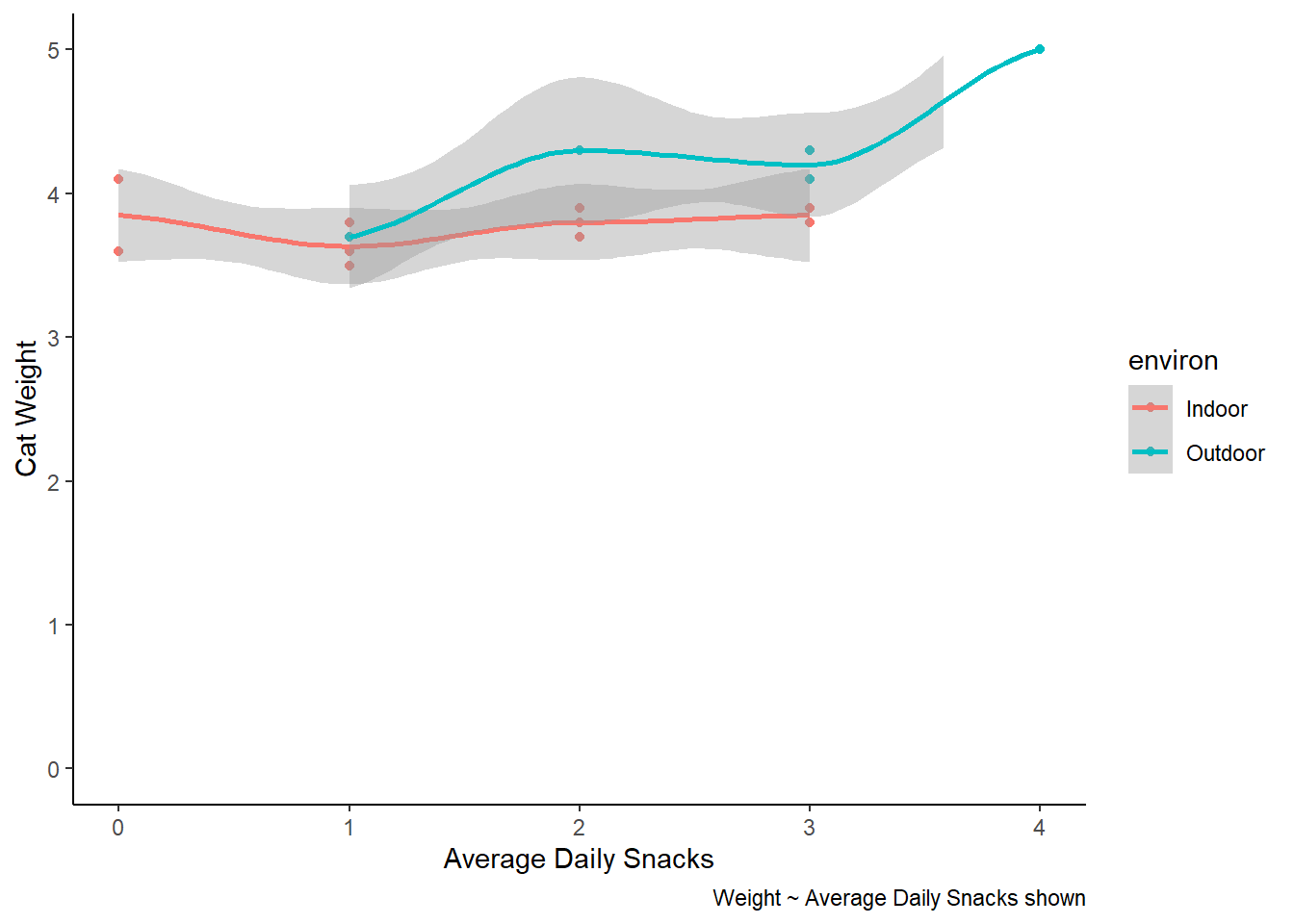
Bayesian Framework
model_bcat2 <- stan_glm(weight ~ avg_daily_snacks + environ, data = cat_weights)
SAMPLING FOR MODEL 'continuous' NOW (CHAIN 1).
Chain 1:
Chain 1: Gradient evaluation took 1.4e-05 seconds
Chain 1: 1000 transitions using 10 leapfrog steps per transition would take 0.14 seconds.
Chain 1: Adjust your expectations accordingly!
Chain 1:
Chain 1:
Chain 1: Iteration: 1 / 2000 [ 0%] (Warmup)
Chain 1: Iteration: 200 / 2000 [ 10%] (Warmup)
Chain 1: Iteration: 400 / 2000 [ 20%] (Warmup)
Chain 1: Iteration: 600 / 2000 [ 30%] (Warmup)
Chain 1: Iteration: 800 / 2000 [ 40%] (Warmup)
Chain 1: Iteration: 1000 / 2000 [ 50%] (Warmup)
Chain 1: Iteration: 1001 / 2000 [ 50%] (Sampling)
Chain 1: Iteration: 1200 / 2000 [ 60%] (Sampling)
Chain 1: Iteration: 1400 / 2000 [ 70%] (Sampling)
Chain 1: Iteration: 1600 / 2000 [ 80%] (Sampling)
Chain 1: Iteration: 1800 / 2000 [ 90%] (Sampling)
Chain 1: Iteration: 2000 / 2000 [100%] (Sampling)
Chain 1:
Chain 1: Elapsed Time: 0.063 seconds (Warm-up)
Chain 1: 0.068 seconds (Sampling)
Chain 1: 0.131 seconds (Total)
Chain 1:
SAMPLING FOR MODEL 'continuous' NOW (CHAIN 2).
Chain 2:
Chain 2: Gradient evaluation took 1.6e-05 seconds
Chain 2: 1000 transitions using 10 leapfrog steps per transition would take 0.16 seconds.
Chain 2: Adjust your expectations accordingly!
Chain 2:
Chain 2:
Chain 2: Iteration: 1 / 2000 [ 0%] (Warmup)
Chain 2: Iteration: 200 / 2000 [ 10%] (Warmup)
Chain 2: Iteration: 400 / 2000 [ 20%] (Warmup)
Chain 2: Iteration: 600 / 2000 [ 30%] (Warmup)
Chain 2: Iteration: 800 / 2000 [ 40%] (Warmup)
Chain 2: Iteration: 1000 / 2000 [ 50%] (Warmup)
Chain 2: Iteration: 1001 / 2000 [ 50%] (Sampling)
Chain 2: Iteration: 1200 / 2000 [ 60%] (Sampling)
Chain 2: Iteration: 1400 / 2000 [ 70%] (Sampling)
Chain 2: Iteration: 1600 / 2000 [ 80%] (Sampling)
Chain 2: Iteration: 1800 / 2000 [ 90%] (Sampling)
Chain 2: Iteration: 2000 / 2000 [100%] (Sampling)
Chain 2:
Chain 2: Elapsed Time: 0.059 seconds (Warm-up)
Chain 2: 0.044 seconds (Sampling)
Chain 2: 0.103 seconds (Total)
Chain 2:
SAMPLING FOR MODEL 'continuous' NOW (CHAIN 3).
Chain 3:
Chain 3: Gradient evaluation took 9e-06 seconds
Chain 3: 1000 transitions using 10 leapfrog steps per transition would take 0.09 seconds.
Chain 3: Adjust your expectations accordingly!
Chain 3:
Chain 3:
Chain 3: Iteration: 1 / 2000 [ 0%] (Warmup)
Chain 3: Iteration: 200 / 2000 [ 10%] (Warmup)
Chain 3: Iteration: 400 / 2000 [ 20%] (Warmup)
Chain 3: Iteration: 600 / 2000 [ 30%] (Warmup)
Chain 3: Iteration: 800 / 2000 [ 40%] (Warmup)
Chain 3: Iteration: 1000 / 2000 [ 50%] (Warmup)
Chain 3: Iteration: 1001 / 2000 [ 50%] (Sampling)
Chain 3: Iteration: 1200 / 2000 [ 60%] (Sampling)
Chain 3: Iteration: 1400 / 2000 [ 70%] (Sampling)
Chain 3: Iteration: 1600 / 2000 [ 80%] (Sampling)
Chain 3: Iteration: 1800 / 2000 [ 90%] (Sampling)
Chain 3: Iteration: 2000 / 2000 [100%] (Sampling)
Chain 3:
Chain 3: Elapsed Time: 0.058 seconds (Warm-up)
Chain 3: 0.053 seconds (Sampling)
Chain 3: 0.111 seconds (Total)
Chain 3:
SAMPLING FOR MODEL 'continuous' NOW (CHAIN 4).
Chain 4:
Chain 4: Gradient evaluation took 3e-05 seconds
Chain 4: 1000 transitions using 10 leapfrog steps per transition would take 0.3 seconds.
Chain 4: Adjust your expectations accordingly!
Chain 4:
Chain 4:
Chain 4: Iteration: 1 / 2000 [ 0%] (Warmup)
Chain 4: Iteration: 200 / 2000 [ 10%] (Warmup)
Chain 4: Iteration: 400 / 2000 [ 20%] (Warmup)
Chain 4: Iteration: 600 / 2000 [ 30%] (Warmup)
Chain 4: Iteration: 800 / 2000 [ 40%] (Warmup)
Chain 4: Iteration: 1000 / 2000 [ 50%] (Warmup)
Chain 4: Iteration: 1001 / 2000 [ 50%] (Sampling)
Chain 4: Iteration: 1200 / 2000 [ 60%] (Sampling)
Chain 4: Iteration: 1400 / 2000 [ 70%] (Sampling)
Chain 4: Iteration: 1600 / 2000 [ 80%] (Sampling)
Chain 4: Iteration: 1800 / 2000 [ 90%] (Sampling)
Chain 4: Iteration: 2000 / 2000 [100%] (Sampling)
Chain 4:
Chain 4: Elapsed Time: 0.055 seconds (Warm-up)
Chain 4: 0.045 seconds (Sampling)
Chain 4: 0.1 seconds (Total)
Chain 4: summary(model_bcat2)
Model Info:
function: stan_glm
family: gaussian [identity]
formula: weight ~ avg_daily_snacks + environ
algorithm: sampling
sample: 4000 (posterior sample size)
priors: see help('prior_summary')
observations: 16
predictors: 3
Estimates:
mean sd 10% 50% 90%
(Intercept) 3.5 0.1 3.4 3.5 3.7
avg_daily_snacks 0.2 0.1 0.1 0.2 0.2
environOutdoor 0.3 0.2 0.1 0.3 0.5
sigma 0.3 0.1 0.2 0.3 0.4
Fit Diagnostics:
mean sd 10% 50% 90%
mean_PPD 3.9 0.1 3.8 3.9 4.1
The mean_ppd is the sample average posterior predictive distribution of the outcome variable (for details see help('summary.stanreg')).
MCMC diagnostics
mcse Rhat n_eff
(Intercept) 0.0 1.0 3785
avg_daily_snacks 0.0 1.0 3047
environOutdoor 0.0 1.0 2937
sigma 0.0 1.0 2680
mean_PPD 0.0 1.0 3807
log-posterior 0.0 1.0 1463
For each parameter, mcse is Monte Carlo standard error, n_eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence Rhat=1).describe_posterior(model_bcat2) Summary of Posterior Distribution
Parameter | Median | 95% CI | pd | ROPE | % in ROPE | Rhat | ESS
------------------------------------------------------------------------------------------------
(Intercept) | 3.53 | [ 3.25, 3.81] | 100% | [-0.04, 0.04] | 0% | 1.000 | 3785.00
avg_daily_snacks | 0.16 | [ 0.02, 0.30] | 98.90% | [-0.04, 0.04] | 1.55% | 1.001 | 3047.00
environOutdoor | 0.28 | [-0.04, 0.62] | 95.65% | [-0.04, 0.04] | 4.18% | 1.000 | 2937.00report::report(model_bcat2)
SAMPLING FOR MODEL 'continuous' NOW (CHAIN 1).
Chain 1:
Chain 1: Gradient evaluation took 1.6e-05 seconds
Chain 1: 1000 transitions using 10 leapfrog steps per transition would take 0.16 seconds.
Chain 1: Adjust your expectations accordingly!
Chain 1:
Chain 1:
Chain 1: Iteration: 1 / 2000 [ 0%] (Warmup)
Chain 1: Iteration: 200 / 2000 [ 10%] (Warmup)
Chain 1: Iteration: 400 / 2000 [ 20%] (Warmup)
Chain 1: Iteration: 600 / 2000 [ 30%] (Warmup)
Chain 1: Iteration: 800 / 2000 [ 40%] (Warmup)
Chain 1: Iteration: 1000 / 2000 [ 50%] (Warmup)
Chain 1: Iteration: 1001 / 2000 [ 50%] (Sampling)
Chain 1: Iteration: 1200 / 2000 [ 60%] (Sampling)
Chain 1: Iteration: 1400 / 2000 [ 70%] (Sampling)
Chain 1: Iteration: 1600 / 2000 [ 80%] (Sampling)
Chain 1: Iteration: 1800 / 2000 [ 90%] (Sampling)
Chain 1: Iteration: 2000 / 2000 [100%] (Sampling)
Chain 1:
Chain 1: Elapsed Time: 0.043 seconds (Warm-up)
Chain 1: 0.048 seconds (Sampling)
Chain 1: 0.091 seconds (Total)
Chain 1:
SAMPLING FOR MODEL 'continuous' NOW (CHAIN 2).
Chain 2:
Chain 2: Gradient evaluation took 1.1e-05 seconds
Chain 2: 1000 transitions using 10 leapfrog steps per transition would take 0.11 seconds.
Chain 2: Adjust your expectations accordingly!
Chain 2:
Chain 2:
Chain 2: Iteration: 1 / 2000 [ 0%] (Warmup)
Chain 2: Iteration: 200 / 2000 [ 10%] (Warmup)
Chain 2: Iteration: 400 / 2000 [ 20%] (Warmup)
Chain 2: Iteration: 600 / 2000 [ 30%] (Warmup)
Chain 2: Iteration: 800 / 2000 [ 40%] (Warmup)
Chain 2: Iteration: 1000 / 2000 [ 50%] (Warmup)
Chain 2: Iteration: 1001 / 2000 [ 50%] (Sampling)
Chain 2: Iteration: 1200 / 2000 [ 60%] (Sampling)
Chain 2: Iteration: 1400 / 2000 [ 70%] (Sampling)
Chain 2: Iteration: 1600 / 2000 [ 80%] (Sampling)
Chain 2: Iteration: 1800 / 2000 [ 90%] (Sampling)
Chain 2: Iteration: 2000 / 2000 [100%] (Sampling)
Chain 2:
Chain 2: Elapsed Time: 0.048 seconds (Warm-up)
Chain 2: 0.039 seconds (Sampling)
Chain 2: 0.087 seconds (Total)
Chain 2:
SAMPLING FOR MODEL 'continuous' NOW (CHAIN 3).
Chain 3:
Chain 3: Gradient evaluation took 9e-06 seconds
Chain 3: 1000 transitions using 10 leapfrog steps per transition would take 0.09 seconds.
Chain 3: Adjust your expectations accordingly!
Chain 3:
Chain 3:
Chain 3: Iteration: 1 / 2000 [ 0%] (Warmup)
Chain 3: Iteration: 200 / 2000 [ 10%] (Warmup)
Chain 3: Iteration: 400 / 2000 [ 20%] (Warmup)
Chain 3: Iteration: 600 / 2000 [ 30%] (Warmup)
Chain 3: Iteration: 800 / 2000 [ 40%] (Warmup)
Chain 3: Iteration: 1000 / 2000 [ 50%] (Warmup)
Chain 3: Iteration: 1001 / 2000 [ 50%] (Sampling)
Chain 3: Iteration: 1200 / 2000 [ 60%] (Sampling)
Chain 3: Iteration: 1400 / 2000 [ 70%] (Sampling)
Chain 3: Iteration: 1600 / 2000 [ 80%] (Sampling)
Chain 3: Iteration: 1800 / 2000 [ 90%] (Sampling)
Chain 3: Iteration: 2000 / 2000 [100%] (Sampling)
Chain 3:
Chain 3: Elapsed Time: 0.044 seconds (Warm-up)
Chain 3: 0.041 seconds (Sampling)
Chain 3: 0.085 seconds (Total)
Chain 3:
SAMPLING FOR MODEL 'continuous' NOW (CHAIN 4).
Chain 4:
Chain 4: Gradient evaluation took 9e-06 seconds
Chain 4: 1000 transitions using 10 leapfrog steps per transition would take 0.09 seconds.
Chain 4: Adjust your expectations accordingly!
Chain 4:
Chain 4:
Chain 4: Iteration: 1 / 2000 [ 0%] (Warmup)
Chain 4: Iteration: 200 / 2000 [ 10%] (Warmup)
Chain 4: Iteration: 400 / 2000 [ 20%] (Warmup)
Chain 4: Iteration: 600 / 2000 [ 30%] (Warmup)
Chain 4: Iteration: 800 / 2000 [ 40%] (Warmup)
Chain 4: Iteration: 1000 / 2000 [ 50%] (Warmup)
Chain 4: Iteration: 1001 / 2000 [ 50%] (Sampling)
Chain 4: Iteration: 1200 / 2000 [ 60%] (Sampling)
Chain 4: Iteration: 1400 / 2000 [ 70%] (Sampling)
Chain 4: Iteration: 1600 / 2000 [ 80%] (Sampling)
Chain 4: Iteration: 1800 / 2000 [ 90%] (Sampling)
Chain 4: Iteration: 2000 / 2000 [100%] (Sampling)
Chain 4:
Chain 4: Elapsed Time: 0.048 seconds (Warm-up)
Chain 4: 0.075 seconds (Sampling)
Chain 4: 0.123 seconds (Total)
Chain 4: We fitted a Bayesian linear model (estimated using MCMC sampling with 4 chains
of 2000 iterations and a warmup of 1000) to predict weight with
avg_daily_snacks and environ (formula: weight ~ avg_daily_snacks + environ).
Priors over parameters were all set as normal (mean = 0.00, SD = 0.80; mean =
0.00, SD = 1.87) distributions. The model's explanatory power is substantial
(R2 = 0.50, 95% CI [0.17, 0.74], adj. R2 = 0.26). The model's intercept,
corresponding to avg_daily_snacks = 0 and environ = Indoor, is at 3.53 (95% CI
[3.25, 3.81]). Within this model:
- The effect of avg daily snacks (Median = 0.16, 95% CI [0.02, 0.30]) has a
98.90% probability of being positive (> 0), 97.72% of being significant (>
0.02), and 76.35% of being large (> 0.11). The estimation successfully
converged (Rhat = 1.001) and the indices are reliable (ESS = 3047)
- The effect of environ [Outdoor] (Median = 0.28, 95% CI [-0.04, 0.62]) has a
95.65% probability of being positive (> 0), 94.53% of being significant (>
0.02), and 85.28% of being large (> 0.11). The estimation successfully
converged (Rhat = 1.000) and the indices are reliable (ESS = 2937)
Following the Sequential Effect eXistence and sIgnificance Testing (SEXIT)
framework, we report the median of the posterior distribution and its 95% CI
(Highest Density Interval), along the probability of direction (pd), the
probability of significance and the probability of being large. The thresholds
beyond which the effect is considered as significant (i.e., non-negligible) and
large are |0.02| and |0.11| (corresponding respectively to 0.05 and 0.30 of the
outcome's SD). Convergence and stability of the Bayesian sampling has been
assessed using R-hat, which should be below 1.01 (Vehtari et al., 2019), and
Effective Sample Size (ESS), which should be greater than 1000 (Burkner, 2017).posteriors2 <- get_parameters(model_bcat2)
posteriors2 |>
pivot_longer(cols = c(avg_daily_snacks, environOutdoor),
names_to = "Parameter",
values_to="estimate") |>
ggplot() +
geom_density(aes(x = estimate, fill = Parameter)) +
theme_classic() +
labs(x = "Posterior Coefficient Estimates",
y = "Density") +
facet_wrap(facets = ~Parameter, ncol = 1) +
theme(legend.position = "none")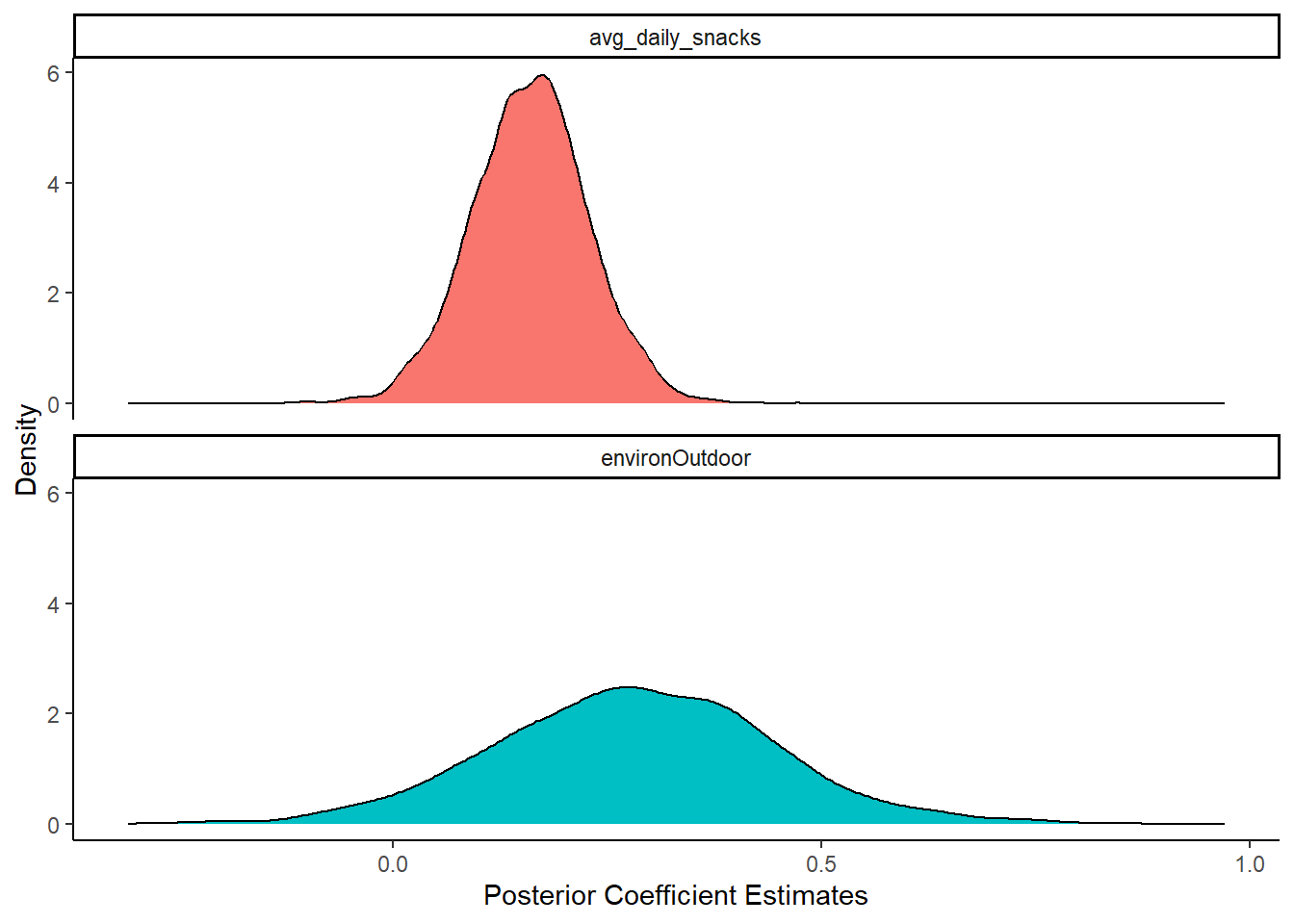
Lecture: Calculating variance
Why does it matter?
vardat <- tibble(cat = c(13, 17, 30, 36, 11, 43, 23, 50, 19, 23),
dog = c(30, 31, 45, 43, 48, 50, 37, 32, 40, 44))
vardat |>
pivot_longer(cols = c(cat, dog),
names_to = "Species",
values_to = "Score") |>
ggplot(aes(x = Species)) +
geom_point(aes(y = Score, colour = Species), position = position_jitter(width = .13), size = 1) +
see::geom_violinhalf(aes(y = Score, fill = Species), linetype = "dashed", position = position_nudge(x = .2)) +
geom_boxplot(aes(y = Score, alpha = 0.3, colour = Species), position = position_nudge(x = -.1), width = 0.1, outlier.shape = NA) +
theme_classic() +
labs(x = "Species", y = "Score") +
theme(legend.position = "none") +
coord_flip()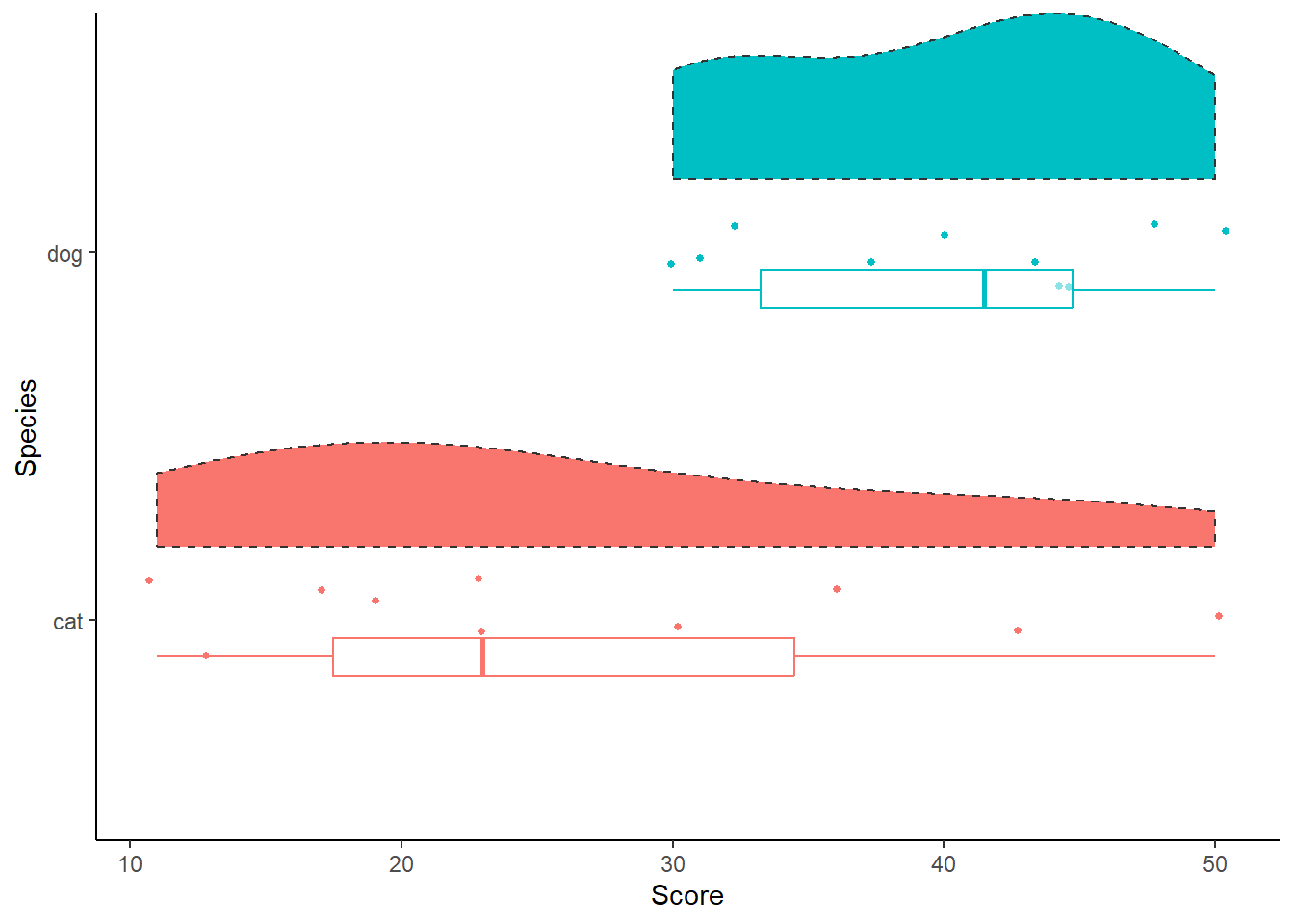
Residuals
resid <- tibble(x = c(1, 2, 3),
y = c(3, 2, 6))
resid |>
ggplot(aes(x, y)) +
geom_point(size = 4, colour = "lightblue") +
theme_classic() +
geom_hline(yintercept = 3.67) +
labs(title = "Plot of 3 points, mean of y shown") +
theme(axis.text.x=element_blank(),
axis.ticks.x=element_blank(),
axis.title.x = element_blank())
Adding the residuals
resid |>
ggplot(aes(x, y)) +
geom_point(size = 4, colour = "lightblue") +
theme_classic() +
geom_hline(yintercept = 3.67) +
geom_segment(aes(x = 1, y = 3.67, xend = 1, yend = 3)) +
geom_segment(aes(x = 2, y = 3.67, xend = 2, yend = 2)) +
geom_segment(aes(x = 3, y = 3.67, xend = 3, yend = 6)) +
labs(title = "Plot of 3 points, mean of y shown, residuals shown") +
theme(axis.text.x=element_blank(),
axis.ticks.x=element_blank(),
axis.title.x = element_blank())
Compare Variances
vardat |>
summarise(var_dogs = var(dog),
var_cat = var(cat))# A tibble: 1 × 2
var_dogs var_cat
<dbl> <dbl>
1 52 169.Compare Standard Deviations
vardat |>
summarise(sd_dogs = sd(dog),
sd_cat = sd(cat))# A tibble: 1 × 2
sd_dogs sd_cat
<dbl> <dbl>
1 7.21 13.0Compare Standard Errors
std.error <- function(x) sd(x)/sqrt(length(x))
vardat |>
summarise(se_dogs = std.error(dog),
se_cat = std.error(cat))# A tibble: 1 × 2
se_dogs se_cat
<dbl> <dbl>
1 2.28 4.11Lecture: Meta Analyses
Calculate rs from R2
sqrt(0.11)